\(\newcommand{\thetitle}{Topology as a theory of Touching} \newcommand{\touches}{\mathrel{\delta}} \newcommand{\ntouches}{\mathrel{\not\delta}} \newcommand{\setdiff}{\mathop{\backslash}} \newcommand{\U}{{\mathcal{U}}} \newcommand{\touchesy}{\mathrel{\delta_Y}}\)
Topological spaces are monoliths, but as with many mathematical phenomena, we can talk about fragments of them. In this case the fragments of interest are \(\textit{subspaces}\), and there are plenty of them. How many? Well, Given a topological space \((\U,\touches)\), which is some ``universe'' set plus it's touching relation, there is a subspace corresponding to each subset of the universe. But the subset alone doesn't wholely determine the subspace: we also need to know it's topological structure, and it would be nice to know ``why that structure?''.
As usual, I was a bit boggled by the definition of subspaces from Munkres. The textbook says that, given a topological space, defined by a universe \(\U\) and a set of open sets \(O\), any subset \(Y \subseteq \U\) induces a subspace toplogy \((Y,O_Y)\), who's open sets \(O_Y\) can be defined as follows: \[ O_Y = \{R \cap Y \text{ for } R \in O\} \] In words, the open sets of subspace Y are exactly those sets that can be formed by intersecting \(Y\) with some open set \(R\) of \(\U\). Ooookay, based on the rules Munkres lays down for the open sets of a topological space, this sure seems to define a topological space over Y:
- The empty set is still a member of \(O_Y\) since \(\emptyset \in O\) and \(\emptyset \cap Y = \emptyset\).
- The entire set \(Y\) is open since \(\U\) is open and \(\U \cap Y = Y\).
- \(O_Y\) is closed over arbitrary unions of its elements. To see this, observe that in general, set intersection distributes through arbitrary set union, i.e., for any set of sets \(Q\) and any set \(A\), \((\bigcup_{q \in Q}q) \cap A = \bigcup_{q \in Q} q \cap A\). It follows, then, that union of some open sets in \(\U\) intersected with \(Y\) forms the same set as the union of the intersection of each relevant open set with \(Y\), each of which is an element of \(O_Y\)
- A similar argument shows that \(O_Y\) is closed over finite intersection of open sets.
Clearly this topological space \((Y,O_Y)\) is derived from \((U,O)\). But, as usual, even though I can \emph{prove} that the topology that we just constructed on \(Y\) is indeed a topological space, and \(Y\) is indeed a subset of \(\U\), and the construction clearly involved the topology imposed on \(\U\) by its open sets \(O\), I come away with very little intuition for why this might be the right thing to do. Can we fix this? I think we can! To make progress, we recast subspaces in terms of touching, and I'm pleased to report that the results are pretty satisfying. I think there is more insight to uncover, though, but I'll save that for a future post.
Recall that a set is open if and only if every element of that set does not touch ``the outside'' (i.e. the complement of the set). So then, given some \(Y \subseteq \U\), what kind of touching relation does the intersection construction above correspond to? I'm happy to report that its description is just as, if not moreso, compelling: If \(\touches\) is the touching relation corresponding to open sets \(O\), then the touching relation \(\touches_Y\) corresponding to open sets \(O_Y\) is just the restriction of \(\touches\) to exactly those pairs \(a \touches A\) such that \(a \in Y\) and \(A \subseteq Y\). In math: \[\forall a\in Y, A \subseteq Y.\, a \touches_Y A \iff a \touches A.\]
I find this \(\textit{very}\) satisfying, because in the open set-based definition, the new open sets \(O_Y\) are related but \emph{not the same as} the open sets \(O\). Some subsets of \(Y\) were \emph{not} open in \(\U\), but now are in \(Y\). You have to do some work, and keep in your mind the original topological space to understand the new one. In contrast, the touching relation for a subspace has \emph{exactly the same touching relationships} as the superspace. Nothing changed, we just restricted our perspective.
Ok, we're actually on the hook to prove that \(O_Y\) and \(\touchesy\) define the same topological space. Honest confession: it took me a looong time to prove this to my satisfaction, and as is often the case, when I finally got one (of too many) proofs to go through, I was miffed that it took me so long (on the upside I learned \emph{a bunch} from getting multiple proofs to go through: each had a different structure which highlighted a different insight).
Here is the most expedient proof, and I think it is still insightful. First, we flip to closed sets: \[ C_Y = \{Y \setdiff (R \cap Y) \text{ for } R \in O\} \]
Every closed set is the complement of some open set, so we build on the definition of \(O_Y\). From here, we can apply some some set-theoretic algebra, keeping in mind that \(Y\) is a subset of \(\U\): \[ Y \setdiff (R \cap Y) = (\U \cap Y) \setdiff (R \cap Y) = (\U \setdiff R) \cap Y \]
And since \(R\) is open in \(\U\), that means that \(\U \setdiff R\) is closed in \(\U\)! So, taking \(C\) as the closed sets of \(\U\), \[ C_Y = \{R \cap Y \text{ for } R \in C\}. \]
It's kind of comforting that we get the closed sets of the subspace using the same construction as we used to get its open sets, but we still have this annoying property that some closed subsets of \(Y\) are not closed subsets of \(\U\). This is where switching to reasoning about the \emph{closure} of an arbitrary subset of \(Y\) pays great dividends. By definition of touching, if \(a \in Y\) and \(A \subseteq Y\), then \(a \touchesy A \iff a \in \mathop{\textit{closure}_Y}(A)\), and \(a \in \mathop{\textit{closure}_Y}(A) \iff a \in \mathop{\textit{closure}}(A)\) To summarize, the subspace topology does not preserve open sets, nor does it preserve closed sets, but it \emph{does} preserve \emph{and reflect} touching.
A Directed Graph Example
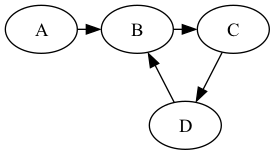
To get some sense of how subspaces work, let's see how directed graphs and topologies induced by them manifest subspacing. For this example, we return to the ``Fallen P'' graph from my previous post on connectivity:
and we focus on Ahlborn's default topology, wherein a node \(a\) of the graph touches a set of nodes \(A\) if and only if the \(a\) is reachable from \(A\). So for instance, in the Fallen P graph, \(C\touches\{A,D\}\).
Adapting the idea of subspace to Ahlborn's default topology, a subspace is incuded by some subset of the nodes. However, directed graphs themselves have a notion of \emph{subgraph}, which is some subset of the nodes of the original graph combined with some subset of the edges among the kept nodes.
A particularly interesting kind of subgraph is the \(\textit{induced subgraph}\) which is what you get when you keep certain nodes of the original graph, and then proceed to retain all of the edges of the original graph that span keptnodes. For instance, if we keep nodes \(A,C,D\), having discarded only node \(B\), we get the following induced graph.
The only remaining edge in the graph connects \(C\) to \(D\) because every other edge involved \(B\) which has been voted out of the archipelago.
Things get interesting, however, when we consider the touching relation of the \(\textit{subspace}\) induced by \(A,C,D\), rather than the edges and paths of the similarly-induced \(\textit{subgraph}\). Since all still-relevant touching relationships are preserved by taking a subspace, we \(\textit{still}\) have \(C\touches\{A,D\}\), which means intuitively that \(C\) is reachable from \(\{A,D\}\). At the least, this means that the Ahlborn default topology induced by an induced subgraph \emph{need not} coincide with the subspace topology induced by considering the same nodes of the original graph and its topology. Curious!
To be honest this is contrary to what I had originally guessed would happen. But on further consideration this makes sense. In my post on connectivity, we observed that if you add new edges to a graph that represent every self-loop and path among nodes, i.e., ensure that there is an edge from each node to each \(\textit{reachable}\) node:
then the resulting graph, which I'll call the ``Monster P'' graph, induces the same Ahlborn default topology as the original. So the topology does not distinguish between edges and paths. There is no ``metric'' for connectivity: \(0\) to \(n\) ``hops'' along edges, for any \(n\), are indistinguishable.
Now consider the subgraph induced by \(A,C,D\) from this monstrosity:
Since the ``Monster P'' graph reifies all instances of reachability as direct edges, the present induced subgraph preserves all of the reachability relationships from the ``Fallen P'' graph. As such, its induced Ahlborn default space is the same as the subspace topology induced by \(A,C,D\) from the original ``Fallen P'''s Ahlborn default topology. So the sense in which the subspace construction preserves the topological structure of the retained nodes seems to be fundamentally about preserving reachability, with no conception of which actual edges of the original graph contribute to that reachability. An interesting abstraction!